Operare con le matrici in C++

Il concetto di matrice viene definito nell’algebra lineare, che è quella branca della matematica che, fra le altre cose, si occupa dello studio delle principali regole per la manipolazione dei vettori e delle matrici. Le matrici sono fondamentali per lo studio dei sistemi di equazioni lineari e rivestono un ruolo importante non solo nella matematica, ma in un ambito molto più vasto, in quanto essenziali in molteplici applicazioni della fisica e dell’ingegneria.

 In questo articolo opereremo con le matrici in C++, prima però sarà necessario introdurre alcune definizioni.

Definizioni

In matematica una matrice è un insieme di numeri disposti su righe e colonne, ad esempio:

A è una matrice formata da 2 righe e 3 colonne.

La dimensione di una matrice si esprime con il numero di righe x numero di colonne. La matrice precedente si dice essere più comunemente una matrice 2×3 o, in maniera equivalente, una matrice di tipo (2, 3). L’elemento di una matrice appartenente alla riga i-esima e alla colonna j-esima si indica con:

Nel caso della matrice precedente: a₁₁=2, a₁₂=3,  a₁₃=1, a₂₁=4, a₂₂=-7, a₂₃=5.

Due matrici si dicono uguali se hanno ordinatamente uguali tutti i loro elementi.

I vettori sono delle matrici particolari formate da una sola riga o da una sola colonna:

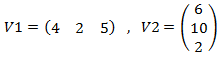
V1 è un vettore riga di dimensione 1×3, V2 è un vettore colonna di dimensione 3×1.

Alcune matrici particolari sono:

• la matrice nulla: composta da elementi tutti nulli;
• la matrice quadrata: quando il n. di righe coincide con quello delle colonne;
• la matrice diagonale: è una matrice quadrata avente tutti gli elementi uguali a zero, eccetto quelli sulla diagonale principale

a_ij=0 per i diverso da j

• la matrice identità: caso particolare di matrice diagonale avente tutti gli elementi della diagonale principale uguali a 1

a_ij=0 per i diverso da j   e   a_ij=1 per i = j

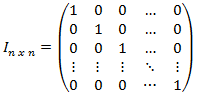
• la matrice simmetrica: una matrice quadrata con a_ij=a_ji per ogni i e j, con i diverso da j

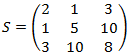
• la matrice triangolare: una matrice quadrata i cui elementi al di sopra (triangolare inferiore) o al di sotto (triangolare superiore) della diagonale sono tutti nulli. Ad esempio, la seguente matrice T è triangolare superiore:

 Algebra delle matrici

• Somma di due matrici

Siano A e B due matrici m x n, ossia (attenzione) con le stesse dimensioni. La somma di A e di B  è una matrice C m x n i cui elementi sono la somma degli elementi aventi la stessa posizione in A e in B:

c_ij=a_ij+b_ij       per ogni i e j

Per la somma di due matrici valgono le seguenti proprietà:

• A+(B+C) = (A+B)+C    è ASSOCIATIVA
• A+B = B+A                  è COMMUTATIVA

 

• Prodotto di un numero reale per una matrice

Sia A una matrice m x n e r un numero reale. Si dice prodotto di r per A la matrice C i cui elementi sono quelli della matrice A moltiplicati per r:

c_ij=ra_ij       per ogni i e j

• Trasposta di una matrice

Sia A una matrice mxn, si dice trasposta di A, e si indica con A^T, la matrice nxm ottenuta da A scambiando ordinatamente le righe con le colonne:

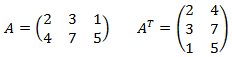
Si fa notare che se una matrice è simmetrica allora A^T=A.

• Prodotto di due matrici

Siano A una matrice mxq e B una matrice qxn, ossia tali che (attenzione) il numero delle colonne della prima matrice sia uguale al numero delle righe della seconda, si definisce matrice prodotto P la matrice i cui elementi p_ij sono ottenuti come somma dei prodotti degli elementi della riga i-esima di A per gli elementi della colonna j-esima di B:

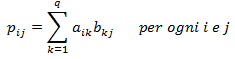
Esempi

1. Prodotto matrice-matrice:

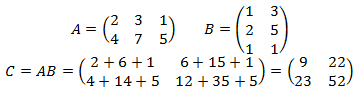
2. Prodotto matrice-vettore colonna

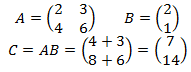
Per il prodotto di due matrici valgono le seguenti proprietà:

• A(BC) = (AB)C    è ASSOCIATIVO
• AB != BA            non è COMMUTATIVO

Operiamo in C++

In informatica una matrice è un array bidimensionale, ossia è una struttura dati che riunisce un insieme di elementi omogenei (ossia dello stesso tipo), ciascuno individuato da due indici, e che può essere rappresentata come una matrice. Per cui il primo indice è detto anche indice di riga, il secondo è detto indice di colonna.

La sintassi C/C++ per dichiarare una matrice è la seguente:

Dopodiché la sintassi per operare con le matrici è quella tipica vista per i vettori, l’unica differenza è che per individuare un elemento della matrice ora non basterà più un solo indice, come avviene per i vettori, ma ne sono necessari due. Con una matrice, inoltre, per avere un accesso sequenziale a tutti i suoi elementi, diventa utilissimo, se non indispensabile, l’utilizzo della struttura di controllo con il due cicli for annidati come nel seguente codice d’esempio, che è bene tenere a mente:

Esempio 1

Scriviamo un semplice programma che dopo aver caricato una matrice, A, di dimension nxm e averla visualizza a video, calcola la trasposta A^T e il prodotto P = AA^T.