C’è un motto latino che recita: “Divide et impera” – dividi e domina – con cui si vuole intendere che «la divisione, la rivalità, la discordia dei popoli soggetti giova a chi vuol dominarli; […] ma anche Luigi XI di Francia usava dire diviser pour régner» (dall’Enciclopedia Treccani).
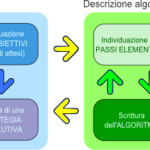
Una strategia questa, dunque, ben nota e già da diversi secoli. In Informatica questo modo di dire indica una metodologia, nota anche come metodologia top-down, utile per affrontare la soluzione di un problema complesso, perché molto efficace per “dominare”, ossia tentare di ridurre, la sua complessità e facilitare così il compito a chi per esso deve trovare una soluzione, cioè progettare l’algoritmo risolutivo. Vedremo che la semplificazione della soluzione del problema è solo uno dei vantaggi che questa metodologia è in grado di apportare. Ma procediamo per gradi e, in questo post, cerchiamo almeno di capire di che cosa si tratta.
L’idea di fondo
I problemi reali spesso si presentano con una complessità tale per cui diventa difficile risolverli se affrontati procedendo allo stesso modo di un problema semplice. Quando la complessità del problema cresce, infatti, diventa faticoso tener conto di tutti gli aspetti coinvolti, valutarne i dettagli e nel contempo prendere decisioni realizzative. Il rischio è quello di perdersi in quello che si deve fare e di non avere più il controllo di ciò che si sta facendo. Nell’affrontare un problema semplice si punta direttamente a trovare una soluzione completa, che consisterà in un algoritmo che può essere descritto con un unico flow-chart (e/o frammento di pseudocodice). Se procedessimo allo stesso modo con un problema complesso, concentrandoci cioè su tutto il problema, per arrivare direttamente ad una sua soluzione completa, otterremmo come soluzione un algoritmo descritto con un unico flow-chart (e/o frammento di pseudocodice) molto esteso, all’interno del quale diventa difficile già solo orientarsi per capirne il funzionamento, sempre ammesso di riuscire a progettarlo. Potrebbe essere più saggio, invece, tentare di ottenere qualcosa di equivalente dalla composizione delle parti più semplici in cui esso può essere scomposto e che, una volta individuate, possano essere comodamente realizzate singolarmente e in maniera indipendente. Bisognerà solo stare attenti a farlo opportunamente, e cioè in modo che ciascuna di queste parti possa essere utilizzata nella composizione finale, ed in modo che tutto funzioni correttamente. Ma cosa nello specifico ciò voglia dire lo chiariremo meglio fra poco con un esempio.
In definitiva, l’idea di fondo su cui si basa la metodologia top-down è questa: se un problema complesso viene scomposto nei suoi sottoproblemi (di dimensioni più ridotte – divide) e, quindi, più semplici da risolvere, ecco che la complessità del problema può essere “dominata” (impera). Dato un problema complesso, quindi, risolverlo applicando la metodologia top-down, vuol dire scomporlo nei suoi sottoproblemi più semplici, che risolviamo separatamente ed in modo tale da poter combinare insieme le loro soluzioni, al fine di determinare la soluzione del problema di partenza.
Esempio
Per chiarire questi concetti, può essere utile considerare un esempio: Il maggiore di una sequenza di numeri.
Osservazioni
Nell’esempio precedente, dopo aver individuato il sottoproblema, prima di tutto ci siamo concentrati sul problema generale disinteressandoci completamente di come risolvere il sottoproblema e stabilendo per esso solo che cosa doveva risolvere. Questo ha estremamente facilitato la soluzione del problema generale.
Alla soluzione del sottoproblema, invece, ci siamo dedicati solo in seconda battuta e lo abbiamo fatto potendoci concentrare solo su di esso e, sicuramente, col vantaggio di trovarci di fronte ad un problema più semplice di quello di partenza.
Si può intuire come con questo modo di procedere, in generale, si ha la possibilità di snellire e semplificare il lavoro di progettazione di un algoritmo: all’inizio, perché permette di ridurre i dettagli del problema da affrontare (processo di astrazione che riduce la complessità del problema) e anche successivamente, perché permette di “diluire” gli sforzi di progettazione, distribuendoli dal problema di partenza più complesso, ai suoi sottoproblemi più semplici.
E’ bene precisare che in informatica la metodologia top-down si fonda su una teoria ed una pratica di programmazione ben consolidate e che in questo post ad essa si è solo accennato. Questa metodologia verrà descritta in maniera più approfondita nei prossimi post.