Problema ‘Stabilire se un numero è primo’

Problema. Dato un numero intero n > 1, stabilire se è un numero primo.

Soluzione proposta. La strategia risolutiva per questo problema può basarsi sulla definizione stessa di numero primo: «un numero primo è un numero naturale maggiore di 1 che sia divisibile solamente per 1 e per se stesso». In altri termini potremmo dire che: n è primo se non è divisibile per nessuno degli interi, k, compresi tra 1 e n, estremi esclusi (1<k<n). Potremmo pensare allora di risolvere il problema verificando proprio ciò.

Si noti che la soluzione del problema generale coinvolge la soluzione di un sottoproblema: «stabilire se un numero intero positivo è divisibile per un altro» (che, tra l’altro abbiamo già affrontato: link).

[quote style=”2″ author=””]Potremmo iniziare ad operare sul problema generale ammettendo, per comodità, di sapere già come risolvere il sottoproblema individuato. Questa astrazione ci aiuta a concentrarci sul problema generale.[/quote]

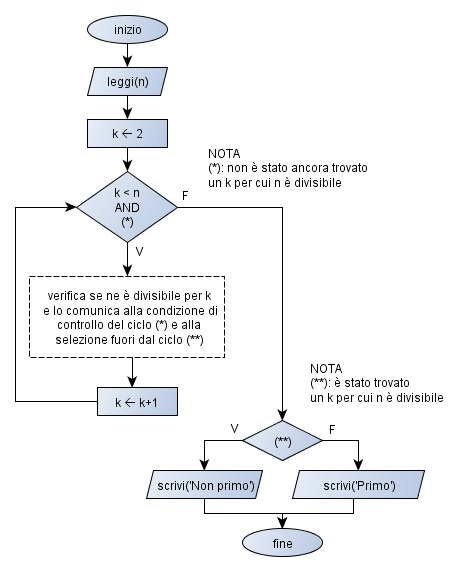
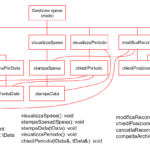
In questo modo la soluzione del problema generale potremmo ottenerla (vedi figura sotto) iterando per k = 2, 3, … n-1 la verifica della divisibilità di n per k: l’iterazione deve continuare fintanto che k risulta minore di n e contemporaneamente non è stato ancora trovato un k per cui n è divisibile (si noti che queste due condizioni si congiungono con un AND logico). Quindi l’iterazione termina quando k raggiunge il valore n e in tal caso si potrà concludere che il numero è primo, oppure prima non appena si trova un valore di k per il quale n risulta divisibile e in tal caso si potrà concludere che il numero non è primo.

Per poter operare in questo modo, però, si deve prevedere un meccanismo di “comunicazione” tra il sottoproblema e il problema generale, che permetta al sottoproblema di informare il problema generale quando viene trovato un k per cui n è divisibile.

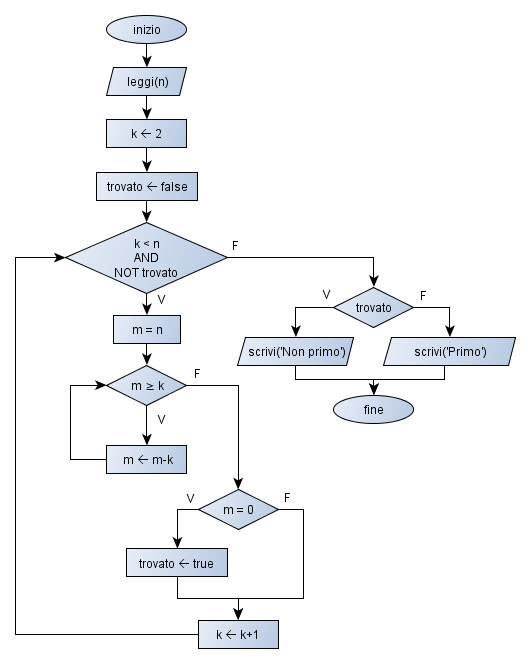
Un modo di procedere può essere utilizzare una variabile flag, ossia una variabile che, opportunamente inizializzata ad un valore fissato, viene impostata su un altro valore fissato, appena si trova un valore di k per cui n è divisibile. Potremmo, per esempio, utilizzare una variabile booleana di nome trovato, che inizialmente è impostata a false e che viene poi portata a true al verificarsi della condizione di divisibilità di n per il valore corrente di k. In questo modo la condizione di controllo della ripetizione dell’algoritmo principale diventa: (k<n AND NOT trovato). Si ricorda, infatti, che per come abbiamo fissato il funzionamento della variabile flag, all’inizio trovato è false e, quindi, NOT trovato vale true determinando così l’ingresso nel ciclo; quando, invece, la variabile trovato viene posta a true, NOT trovato vale false e ciò determina l’uscita dal ciclo.

Sin qui abbiamo risolto solo l’algoritmo generale e rimane da risolvere il sottoproblema. Così facendo, però, abbiamo raggiunto il vantaggio di poter concentrare tutti i nostri sforzi sulla soluzione di un problema sicuramente più semplice di quello di partenza. Poiché questo problema è stato già risolto in un altro post (a cui si rimanda: link), qui utilizzeremo direttamente quanto già è stato trovato e per completezza distingueremo i due casi che sono stati considerati in quel post: il primo, in cui si ipotizza che l’esecutore sappia calcolare il resto della divisione intera fra due numeri interi positivi, il secondo, senza questa ipotesi. Ciò che si ottiene viene descritto di seguito in pseudocodice e in flow-chart.

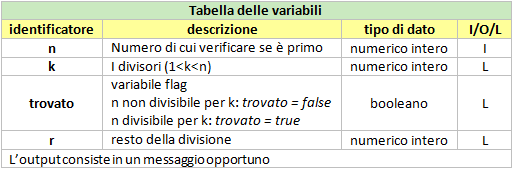
CASO 1: si ipotizza che l’esecutore sappia calcolare il resto della divisione intera fra due numeri interi positivi.

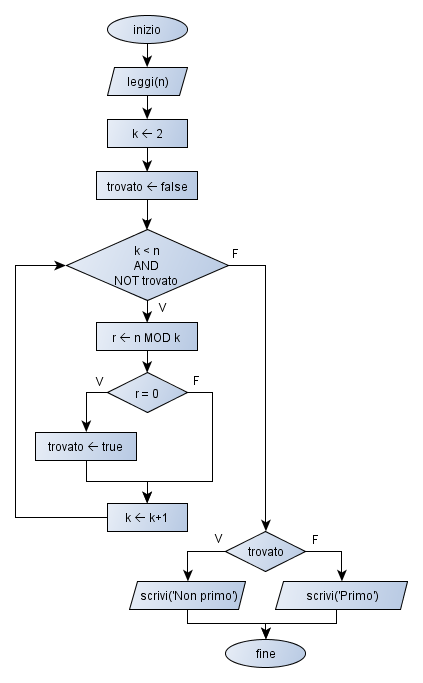
 CASO 2: si ipotizza che l’esecutore non sappia calcolare il resto della divisione intera fra due numeri interi positivi.